Pearsonov koeficient korelacije meri linearno povezanost dveh številskih spremenljivk. Koeficient lahko izračunamo ročno po formuli ali za izračun uporabimo različne statistične programe. Le-ti kot rezultat analize povezanosti običajno izpišejo korelacijsko matriko linearne povezanosti dveh spremenljivk.
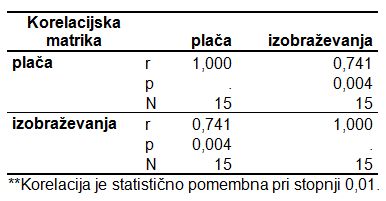
Primer korelacijske matrike, kjer smo 15 zaposlenih (to je velikost našega vzorca, ki ga v korelacijski matriki predstavlja vrednost N) vprašali o višini njihove plače (plača) in številu dodatnih izobraževanj (izobraževanja), katerih so se udeležili v lanskem letu.
S tako pridobljenimi podatki želimo preveriti povezanost med višino plače in udeležbo na dodatnih izobraževanjih.
Kako si razložimo rezultat korelacijske matrike?
Diagonalo korelacijske matrike vedno predstavljajo vrednosti korelacijskega koeficienta 1. Le-ta govori o popolni linearni povezanosti, kar smiselno velja za povezanost spremenljivke same s seboj.
Rezultat analize povezanosti dveh spremenljivk je informacija o vrednosti korelacijskega koeficienta v primeru povezanosti spremenljivke ‘plača’ in ‘izobraževanja’, kjer je vrednost koeficienta v našem primeru 0,741. Glede na lestvico moči povezanosti takšna vrednost pomeni visoko/močno pozitivno povezanost spremenljivk. Vsebinsko to pomeni, da je višina plače zaposlenega povezana z večjim številom dodatnih izobraževanj. Na osnovi tega lahko sklenemo, da imajo zaposleni, ki se večkrat dodatno izobražujejo, višjo plačo oziroma da imajo zaposleni, ki se manjkrat dodatno izobražujejo, nižjo plačo. V kolikor bi bila vrednost koeficienta negativna, bi bili spremenljivki močno negativno povezani. Z vsebinskega vidika bi to pomenilo, da se zaposleni z višjo plačo udeležujejo manj dodatnih izobraževanje oziroma da se zaposleni z nižjo plačo udeležujejo več dodatnih izobraževanj.
Ker je vrednost stopnje značilnosti (kar v zgornji korelacijski matriki kaže vrednost p) manjša od 0,01 pomeni, da je linearna povezanost analiziranih spremenljivk statistično značilna oziroma statistično pomembna. Kaj to pomeni za naš hipotetični vzorec zaposlenih? Vsebinsko to pomeni, da v kolikor bi se višina plače zaposlenih spremenile (zvišale ali znižale), bi se statistično pomembno spremenila (zvišale ali znižale) tudi količina obiskovanja dodatnih izobraževanj.
Informacije o linearni povezanosti dveh spremenljivk lahko pridobimo tudi z grafično predstavitvijo vrednosti spremenljivk. V ta namen uporabimo razsevni grafikon (ang. Scatter plot), ki predstavlja vrednosti ene spremenljivke na osi x in vrednosti druge spremenljivke na osi y. Katero spremenljivko predstavimo na kateri osi je vseeno, saj sta spremenljivki pri analizi povezanosti enakovredni. Grafični rezultat je torej grafikon, na katerem vidimo veliko točk, ki nam enako kot vrednost Pearsonovega korelacijskega koeficienta povedo moč in smer povezanosti teh dveh spremenljivk.
Kako ugotavljamo moč linearne povezanosti na osnovi grafičnega prikaza?
Kot omenjeno na grafu vidite množico točk, ki so tako ali drugače razporejene. V kolikor so te točke razporejene tako, da bi lahko enostavno potegnili bolj ali manj ravno črto med njimi (pri tem vedno dopuščamo odstopanje kakšne točke izven te ravne črte, ki jo je sicer moč tvoriti z večine točk), med spremenljivkama obstaja močna povezanost. V kolikor so te točke med seboj zelo težko povezljive v obliki ravne črte, med spremenljivkama obstaja šibka povezanost.
Kako ugotavljamo smer linearne povezanosti na osnovi grafičnega prikaza?
Razsevni grafikon množice točk vrednosti dveh spremenljivk poda informacijo tudi o tem ali je povezanost med spremenljivkama pozitivna, negativna ali le-te ni.
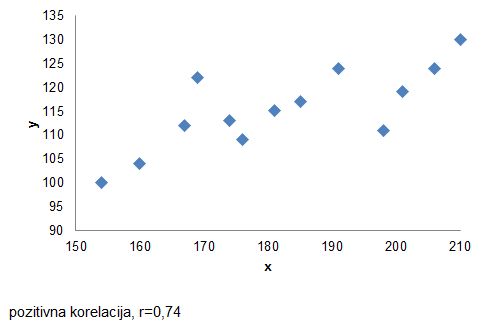
Kadar je povezanost pozitivna, si v grafu lahko predstavljate linijo točk, ki se vzpenja oziroma narašča.
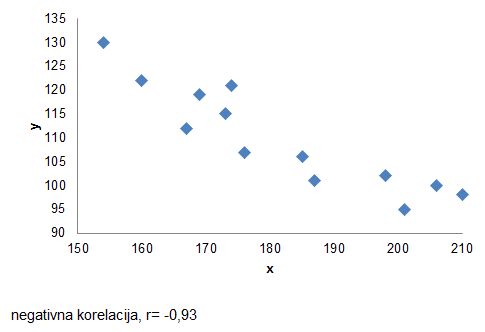
Kadar je povezanost negativna, si v grafu lahko predstavljate linijo, ki se spušča oziroma pada.
Kadar linearne povezanosti ni, so točke na grafu razporejene zelo razpršeno.
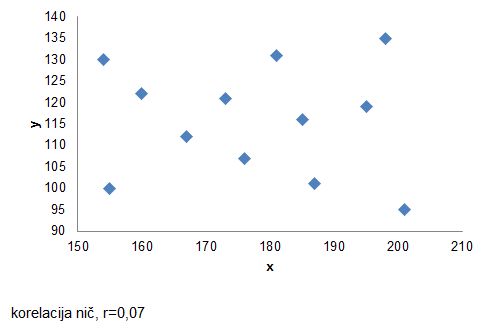
V praksi se uporabljata oba načina preverjanja linearne povezanosti dveh spremenljivk. A pri resni statistični analizi se grafična metoda uporablja zgolj informativno, kot rezultat analize povezanosti dveh spremenljivk pa se upošteva in interpretira koeficient korelacije.
Se ukvarjate s statistično analizo podatkov in potrebujete pomoč? Potrebujete izračun vrednosti korelacijskih koeficientov? V podjetju BenSTAT vam bomo svetovali in poskrbeli za kakovostno analizo vaših podatkov. Oglasite se: info@benstat.si!