Pearsonov koeficient korelacije (r) (ang. Pearson correlation) je najpogosteje uporabljena mera linearne povezanosti (ang. linear correlation) dveh številskih spremenljivk. Predpostavlja uporabo vsaj intervalnega tipa obeh analiziranih spremenljivk in linearno povezanost spremenljivk. Koeficient lahko zavzame vrednosti med -1 in 1. Izračunamo ga s kovarianco Cxy in standardnimi odkloni obeh spremenljivk po spodnji formuli:
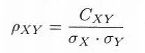
kjer je kovarianca mera linearne povezanosti med spremenljivkama in jo izračunamo po spodnji formuli:
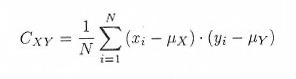
kjer je N velikost vzorca, xi in yi vrednost i-te spremenljivke in µx in µy aritmetična sredina posamezne spremenljivke.
Pearsonov koeficient korelacije nam odgovori na dve vprašanji, in sicer:
- Ali linearna povezanost med spremenljivkama sploh obstaja? in
- Kako močna je linearna povezanost med spremenljivkama?
Kadar preverjamo obstoj linearne povezanosti, govorimo o dveh vrstah povezanosti.
- Pozitivna povezanost (ang. positive correlation) obstaja takrat, kadar so vrednosti prve (x) in druge (y) spremenljivke visoke oz. nizke. Tedaj je koeficient pozitiven in blizu 1. Primer koeficienta pozitivne povezanosti: 0,88.
- Negativna povezanost (ang. negative correlation) obstaja takrat, kadar so vrednosti prve (x) spremenljivke visoke in vrednosti druge (y) spremenljivke nizke oz. obratno. Tedaj je koeficient negativen in blizu -1. Primer koeficienta negativne povezanosti: -0,70.
Kadar ne gre niti za pozitivno niti za negativno povezanost med spremenljivkama rečemo, da spremenljivki med seboj nista linearno povezani (uporabljamo tudi – nista v korelaciji, ne korelirata). Tedaj je koeficient blizu 0.
Pri statističnem sklepanju o korelacijski povezanosti postavimo ničelno in osnovno domnevo, in sicer:
- H0: r = 0, spremenljivki nista linearno povezani,
- H1: r ≠ 0, spremenljivki sta linearno povezani.
Pri tem uporabimo t statistiko, ki jo izračunamo s pomočjo vrednosti korelacijskega koeficienta po spodnji formuli, kjer je r korelacijski koeficient in je n velikost vzorca.
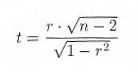
Na osnovi t statistike in izbrane stopnje značilnosti (običajno 0,05) določimo kritično območje. Kadar se vrednost t statistike nahaja v kritičnem območju rečemo, da je ob 5 % stopnji značilnosti prva spremenljivka linearno povezana z drugo spremenljivko.
Za določanje moči povezanosti (ang. correlation strength) spremenljivk uporabljamo spodnjo lestvico vrednosti koeficienta, in sicer:
Vrednost koeficienta -> Moč povezanosti
- 0,00 -> ni povezanosti
- 0,01-0,19 -> neznatna povezanost
- 0,20-0,39 -> nizka/šibka povezanost
- 0,40-0,69 -> srednja/zmerna povezanost
- 0,70-0,89 -> visoka/močna povezanost
- 0,90-0,99 -> zelo visoka/zelo močna povezanost
- 1,00 -> popolna (funkcijska) povezanost
Potrebno je še poudariti, da Pearsonov koeficient korelacije govori o povezanosti dveh spremenljivk, ne pa tudi o vplivu ene spremenljivke na drugo. Interpretacija oziroma rezultat koeficienta je torej »Zadovoljstvo z delovnim mestom in višina plače sta med seboj povezana.«, ne pa tudi »Višja plača vpliva na večje zadovoljstvo z delovnim mestom«, kot je večkrat napačno razlagano.
Pearsonov koeficient korelacije je prvi uporabljal Anglež Francis Galton, Pearsonov profesor in pionir statistične korelacije in regresije, imenuje pa se po britanskem statistiku in matematiku Karlu Pearsonu.
Se ukvarjate s statistično analizo podatkov in potrebujete pomoč? Potrebujete izračun vrednosti korelacijskih koeficientov? V podjetju BenSTAT vam bomo svetovali in poskrbeli za kakovostno analizo vaših podatkov. Oglasite se: info@benstat.si!






