Aritmetična sredina (µ) (tudi Enostavna aritmetična sredina ali Povprečje) je najpogosteje uporabljena mera srednjih vrednosti. Definirana je kot kvocient med vsoto vseh vrednosti spremenljivk na populaciji in skupnim številom enot v populaciji. Lahko jo izračunamo za številske spremenljivke, ki so približno normalno porazdeljene.
Formula za izračun aritmetične sredine, kjer y predstavlja vrednosti številskih spremenljivk in N predstavlja število različnih spremenljivk:
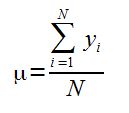
Standardna napaka aritmetične sredine (σM) je standardni odklon vzorčne porazdelitve aritmetičnih sredin in meri natančnost vzorčne ocene aritmetične. Pove nam v kakšnem razponu se vrednosti aritmetičnih sredin populacije gibljejo, kar lahko trdimo z določenim (običajno 95 %) intervalom zaupanja.
Formula za izračun standardne napake aritmetične sredine, kjer σ predstavlja standardni odklon in N predstavlja število različnih spremenljivk:
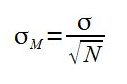
Primer: Šestletni Ben ima pet prijateljev. Dva sta stara enako kot on, torej 6 let, dva sta starejša od njega, eden je star 7, drugi pa 7,5 let, en prijatelj pa je eno leto mlajši, star je torej 5 let. Kakšna je povprečna starost njegovih prijateljev?
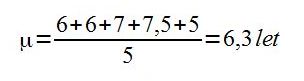
Se ukvarjate s statistično analizo podatkov in potrebujete pomoč? Potrebujete izračun aritmetične sredine in ne razumete pomena standardne napake aritmetične sredine? V podjetju BenSTAT vam bomo svetovali in poskrbeli za kakovostno analizo vaših podatkov. Oglasite se: info@benstat.si!








